树与二叉树的基本了解

树

树的定义

树是一种非线性的数据结构，它是由n个有限结点组成的集合。

• 有一个特殊的结点，称为根结点，根结点没有前驱结点
• 除去根结点外，其余结点被分为M个互不相交的集合T1、T2、······、Tm，其中每一个集合Ti又是一棵子树

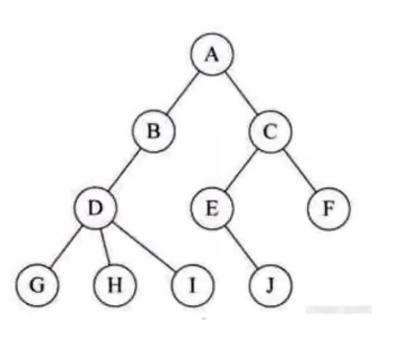
• 结点：树中的一个独立单元
• 父结点/双亲结点与子结点：若一个结点含有子结点，则这个结点称为其子结点的父结点
• 结点的度：结点的子树数量/子结点的数量
• 树的度：一棵树中，最大的结点的度称为树的度
• 叶子结点/终端结点：度为0的结点称为叶结点
• 分支结点/非终端节点：度不为0的结点
• 结点的层次：从根开始定义起，根为第一层，根的子结点为第二层，以此类推

树的性质一

• 树中的结点数 = 所有结点的度数 + 1，以上图为例：图中总共10个结点（ABCDEFGHIJ），结点的总度数是9

• 真题解析：

  一棵度为4的树T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树T的叶子结点个数是？

  答：先算树中结点数：根据公式，树的结点数为123，叶子结点个数为：123-41=82

二叉树

二叉树的定义

• 有且仅有一个称之为根的结点
• 除了根结点以外的其余结点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T1和T2本身又都是二叉树。
• 二叉树不存在度大于2的结点
• 二叉树的子树又左右之分，次序不能颠倒，因此二叉树是有序树

二叉树的性质

• 性质一：二叉树的第 $i$ 层最多有 $2^{i - 1}$ 个结点

• 性质二：深度为 $k$ 的二叉树最多有 $2^k - 1$ 个结点

• 性质三：对于任意一棵二叉树，如果其叶子结点数为 $N_0$，而度数为 2 的结点总数为 $N_2$，则 $N_0 = N_2 + 1$

特殊二叉树-满二叉树

满二叉树定义：深度为 $k$ ，并且含有 $2^{k - 1}$ 个结点的二叉树，这类二叉树每层结点数均达到对应层最多结点数，是特殊的二叉树形态 。

满二叉树性质：

• 叶子结点只能出现在最后一层
• 非叶子结点的度一定是 2
• 同样深度的二叉树中，满二叉树的结点个数最多，叶子结点的数量最多

特殊二叉树-完全二叉树

完全二叉树定义：对一棵具有 $n$ 个结点的二叉树按层序编号，如果编号为 $ i $ 的结点与同样深度的满二叉树中编号为 $ i $ 的结点在二叉树中的位置完全相同，则这棵二叉树称为完全二叉树

完全二叉树的特点：

• 叶子结点只能出现在最下两层。
• 最下层叶子结点一定集中在左部连续位置。
• 倒数第二层若有叶子结点，一定都在右部连续位置。
• 如果结点度为 1，则该结点只有左孩子，即不存在只有右子树的情况。

满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树